« Talking to God .... | Main | Labour melt down? »
March 27, 2006
Getting sidetracked ...
It's been my turn to write for the blog yesterday but somehow I got sidetracked... I have to admit I had a lot of fun all afternoon and I thought you might like to share it with me.
By now it has probably transpired that I am sort of fascinated by numbers. So I got easily hooked by a brain teaser I found in the newspaper: a Kakuro puzzle.
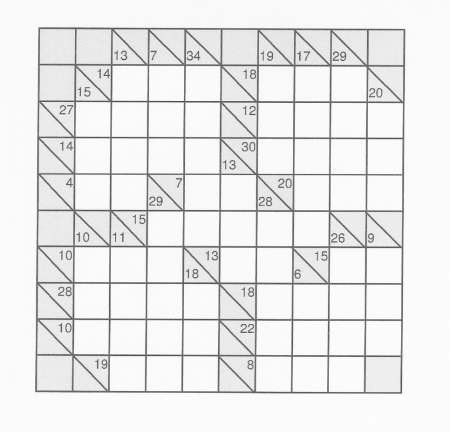
Kakuro puzzle
The rules sound easy: you fill in numbers between 1 and 9 so that the sum of the digits in each row or column equals the number given in the appropriate grey boxes. For example, first row on the left: 14 could be 9+4+1 or 8+5+1 or 7+5+2 etc. You are not allowed to use one the same digit twice for a sum. Sounds dead easy, but I assure you it isn't.
Have a go yourself if you like - I wish you a pleasant time.
Posted by Mausi at March 27, 2006 04:55 PM
Trackback Pings
TrackBack URL for this entry:
http://mt3.mu.nu/mt/mt-tb.cgi/4082
Comments
There is more than one solution. The first three numbers (top left of the grid) could be: 3-2-9 or 4-2-8. Both combinations can fill the top left section completely (with no interactions on the rest of the puzzle.
Posted by: Ozguru at March 27, 2006 07:40 AM
This seems to be impossible, given the rules you have stated: look at the bottom left corner, then up 4 squares - the 2 squares right of the 15 can only be 9 - 6, 8 - 7, 7 - 8, or 6 - 9. The second of those squares sums vertically to 9. None of the above choices allow you to do that - even the lowest (6) needs three 1's, which is an illegal repetition.
Posted by: Steve at March 27, 2006 04:00 PM
Steve, this is why I leave all mathematical problems to Mausi or a computer programme!
Posted by: The Gray Monk at March 27, 2006 04:41 PM
Sigh... and I love these kind of things.
Posted by: vw bug at March 27, 2006 08:30 PM
OK. I have it solved. The diagonal (top left to bottom right) reads: 6163428.
Posted by: Ozguru at March 28, 2006 04:10 AM
Yes, Ozguru, I entirely agree with you about the diagonal. But how does that fit 3-2-9 in the first row?
Posted by: Mausi at March 28, 2006 04:48 AM